Today is Thanksgiving in the U.S.A. I will be celebrating with loved ones Sunday, so don't feel sorry for me working on a holiday. Besides, this post is going to be even more delicious than sweet potatoes with marshmallows, green bean casserole, and Mama Stamberg's Cranberry Relish (my personal favorite) combined.
In honor of this weird holiday – a mélange of harvest celebration, legend, Christian religiosity, gluttony, and tension both familial and historical, I am going to write about the word grateful and its family.
The orthographic structure of that word, grateful, is <grate> +< ful>. The <grate> is a bound base element, distinct from the word grate as in grate cheese, and also distinct from the word grate as in fireplace grate. There are, therefore, three homographic base elements <grate> – two free and one bound. The bound base element in grateful is shared by gratuity, gratuitous, gratitude, ingrate, gratify, and congratulations. Here is a lexical word matrix featuring this family:
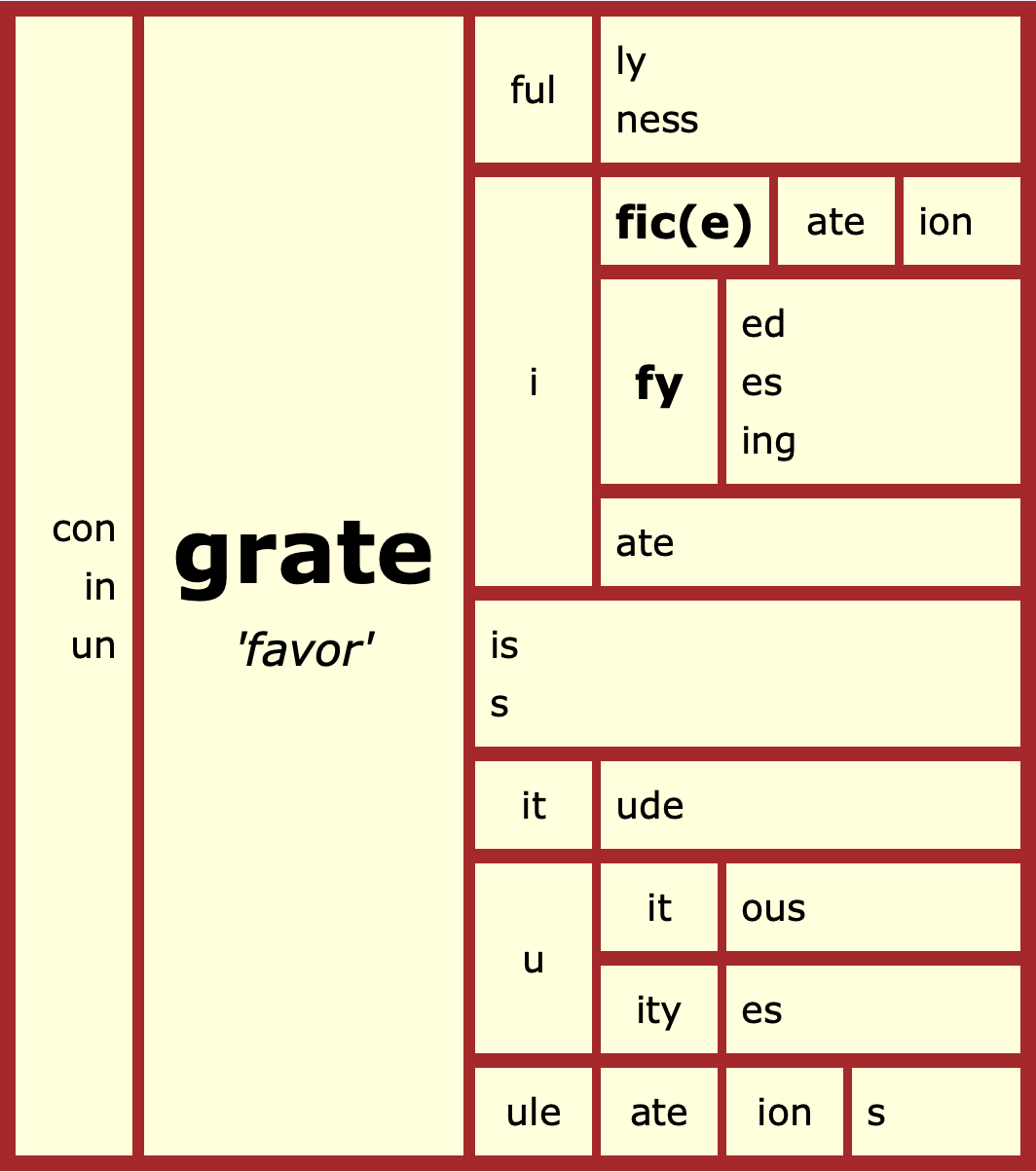
Note that there is no <-ate> suffix in the base element <grate>. Its French cousin/descendant is <grace>, also a base element with no suffix, but a free one. It's not uncommon to find a <c> in French words where there's a <t> in the Latin forebear, like palace~palatial or policy~politician. And yes, I did include <ity> as a suffix – so no, gratuity doesn't have two connecting vowel letters. I will explain the base element in.this post, but the <ity> suffix will have to keep.
Now, it's not just Thanksgiving that interested me in this word family; admin of one of the ginormous, feel-good word study Facebook groups full of thousands of strangers posted a different matrix for this family, falsely claiming that the base element is <gr>, and that the letters <ate> are a suffix. Another self-proclaimed expert who lacks credentials – I'll call him, um, Joe Honduras – posted his own fact-free *<gr> matrix in the comments. They're both wrong, but lots of easily-impressed people in that group who themselves lack the linguistic understanding to fact-check anyone Oohed and Aahed about both matrices. NO ONE thought to challenge the claims in those matrices, and no one in that group has the linguistic chops to check them on their own.
Several people who saw it did, however, think to ask me for help in discerning whether that matrix and its inherent claims were accurate. They're not.
Here's the proof: